Figyelmeztetés: Időközben az adott tételről kiderült, hogy valójában soha sem volt érvényesen bizonyítva és alaplogikai hibás.
..................................
"Gödel, aki matematikus volt, azzal vált híressé, hogy bebizonyította: lehetetlen bebizonyítani minden igaz állítást, még ha olyan száraz, egzakt területre is korlátozzuk magunkat, mint a számtan." Forrás: Stephen Hawking: Az idő rövid története könyv.
A fenti idézet egyértelmű butaságot tartalmaz és ha sokak által a "világ legokosabb emberének" tartott valaki ilyeneket megengedhetett magának a könyvében megjelenni, akkor ne csodálkozzunk, hogy a butaságok szaporodnak és nem a tudományosságok. Sőt végeztem kísérletezést és más tudományágakban képzettek közül is sokan helytelenül értelmezik és nem értik valójában. Tehát érdemes ezt a folyamatot, mint memetikai érdekességet és feltárást is átnézni, mert vannak olyan részei is. Pláne, hogy sok teológus és filozófus, Gödel tételét használja "kardnak" az ókori meséik egyes részeinek alátámasztásául.
Tisztázzuk: Gödel értette a saját első nem teljességi tételét és helyesen. A matematikusok is szinte kivétel nélkül helyesen értelmezik. - Sokan mások nem értik és ezek szerint Hawking sem értette. Vagy értette.... csak???
Mi is volt Hawking végzettsége? Elméleti fizikus? Elvileg nem lett volna szabad ekkorát hibáznia a felkészültsége miatt és pláne nem ilyen lényegi kérdéskörben. Itt több dolog lehetséges:
1. Hawking buta volt és fel sem tudta fogni Gödel első nem teljességi tételét.
2. Hawking nem volt buta felfogta, csak a Pápai Akadémiai Tagsága miatt eltorzította.
3. Hawking nem volt buta csak a könyvkiadója, ahogyan a végét is átírták, tettek bele más bulvár populáris butaságokat is. Például; a Pápai 'Tudományos' Akadémia céljainak támogatása miatt, nem véletlenül ez a befejezése: "Mert akkor megismerhetjük Isten gondolatait" Jómagam ezt a verziót tartom a legvalószínűbbnek. Hawking kettős játszmát végzett, és "egy seggel próbált meg két lovat is megülni". Annyira nem tetszhetett ez neki, de az ígért siker miatt belement.
4. Hawking nem volt buta és az idézete helyes és igaz. (akkor én tévednék, de nem tévedek)
5. Hawking nem volt buta, csak bekapott egy mémet és ez torzította el az éleslátását és másokét is.
6. A magyar nyelvre fordító volt buta és helytelenül fordított.

Kezdjük azzal, hogy ide tesszük Gödel első nem teljességi tételének az ismert legjobb magyar nyelvű szöveges leírását: "Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan állítás, mely se nem bizonyítható, se nem cáfolható."
Igen, ennyi a tömör lényeg, logikai és matematikai hókuszpókolások nélkül és azt kikerülve. Kezdjük el értelmezni mit is jelent ez még közérthetőbben és példákkal, hasonlatokkal. Kb annyit jelent, hogy zöld a fű és kék az ég, a paradoxonok meg paradoxonok, a dogmák meg dogmák. Zárt és kitalált rendszerek belülről számos kérdéskörben nem igazolhatják és nem is cáfolhatják magukat. ... Nem lesz attól igaza Kis Jóskának, mert leírja, hogy neki mindig igaza van. A matek meg kitalált dogmatikus rendszere épül. A {pont} ez és ez ... punktum.... a {nyolc} meg ez és punktum .... Illetve rendszerekre, mert ugyebár csak számrendszerből is van több tucatnyi is, de a legtöbb ember legalább a tízest, kettest, tizenkettest és a hatvanast ismeri. Illetve talán még a római számtan rendszert is. Az egyikben 1+1=2 igaz, a másikban meg hamis állítás. mert ott már például 10 lenne.
A lényeg viszont még egyszer ideidézve, hogy ez hol is érvényes; a "formális-axiomatikus elméletben". Tehát egy nagyon szűk és csak matematikai területen. Hogy káromkodjak; a matematikai aritmetikában.
Más megfogalmazásban: "Fontos megjegyeznem, hogy Gödel tételei csak a matematikai rendszerek egy részében érvényesek, nem alkalmazhatóak a számokat vagy a formális nyelvezetet nélkülöző euklideszi geometriában, humán és társadalomtudományokban vagy bármely hasonló rendszerben." forrás forrás2
Itt igazából már be is fejezhetném fejtágítást, de sajnos elő kell még is rágnom a tejbepapinak valót. Mert nem fogadok, mert tutira tudni lehet, ettől még sokaknak nem esett le a tantusz, hogy akkor ez miért is mond ellent a kezdő Hawking idézettel. Egyszerű halmazelmélet. Ott úgy van leírva, hogy ez általánosan igaz és még ráadásul a matematika legszigorúbb rendszerén belül is. Holott ez fordítva van. Gödel tétele csak a matematikán belül igaz és annak is csak egy szűk részén. Máshol meg nem. Mert ha kilépünk a matematikából, akkor metafizikába vált át a szöveg, ami meg egyértelmű áltudomány és zagyvaság.
Tehát Gödel nem alkotott meta-matematikát, ahogyan Karl Popper sem meta-logikát. Gödel nem ment a matematikán túlra, akkor sem ha elmebetegségével is meg kellett küzdenie, és az nem is sikerült neki. Az első nem teljességi tétele maximum a matematikán belül igaz csak. Sőt, ha rávetítjük saját magára a tételt, hát lehet még azon belül sem. Esetleg egy eldönthetetlen és valódi paradoxont eredményezhet.
............................
Utólagos fejlemény: Gödel első nemteljességi tétele hamis dilemma és spanyol viasz jellegű
Nos úgy néz ki, hogy St. Hawking nem csak rosszul értelmezte Gödel első nemteljességi tételét, hanem eleve az egész hivatkozása alapjaiban hibás, mert a Gödel tétel önmagában is hibás. Tehát számos esetben nem hivatkozhatnak arra a számítások ellentmondásossága miatt.
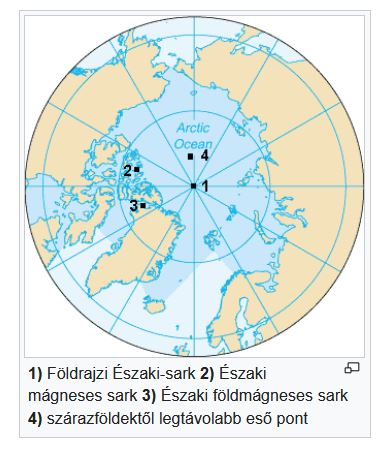
St. Hawking " Nincs semmi a Déli-Sarktól délebbre" hablatyolása körkörös érvelési hiba csak, akárcsak a Hófehérkénél, nincs Hófehérkébb feltételezett tanpélda állítás is az. Ezt a marhaságot sokan másolják, még Északi-Sark variációban is. Másrészt eleve Északi-sarkból több is van és némelyik mászkál is.