Úgy kezdődött hogy néhány matematikus fejébe vette, hogy a MATEK MINDENEK FELETTI, ....ÜBER, ... meg szárazabb érzés. ... Meg a Matek a tudományok führere, császára és királynője. Meg minden tudományok tudománya és alapja. Logikák logikája és mindent lehet vele helyettesíteni, az általános logikus gondolkodást, a filozófiát és a tudományfilozófiát is. Tehát kitalálták úgy köbö 120-140 évvel ezelőtt főként a tudományfilozófiát helyettesíteni kívánó szándékkal a MATEMATIKAI FORMALIZÁLÁST. Aminek később és főként a számítás és irányítástechnika miatt lett jelentős haszna is persze, többek közt Neumann János (1903 -1957) a pricentoni Institute for Advanced Studies matematikus professzora által, de nagy hiba, hogy azt néhányan, ettől eltérő logikai területen túltolták.
Érdekességként megjegyzem, hogy lényeget tekintve Neumann János vette fel az adott egyetemhez Gödelt és Einsteint is alkalmazott kutatónak. Ezen az ott készült képen valószínűleg azért nincs rajta, mert az ő kezében volt a fényképezőgép.

"A matematikai logika és a halmazelmélet két tantárgya a 19. század vége óta tartozik a matematikához. Ezen időszak előtt a halmazokat nem tekintették matematikai objektumoknak, és a logika, bár matematikai bizonyításokhoz használták, a filozófiához tartozott, és a matematikusok nem vizsgálták kifejezetten. ... Még mindig filozófiai vita folyik arról, hogy a matematika tudomány-e." forrás
Vallási Dogma = Matematikai Axióma. A valódi tudományágak éppen ezért nem is használnak axiómákat. ELNEVEZÉS alapúak. Az elnevezéseket meg lehet módosítani, pontosítani, tesztelni, bírálni, és elvetni is.
Igazából nem egy matematika van, ahogyan vallás sem csak egy van, hanem sok matematika és sok és vallás létezik. ( Mono-matematika <-> poli-matematika. ) Amelyek elveikben és szabályaikban, részben, vagy akár teljes egészében, ellenkeznek egymással. A jelenlegi asztrofizika problémáit és anomáliáit, főként az axiomatikus matematika túltolása és túl dimenzionálása okozta és okozza. A matematika a vallások szintjén van, alaphelyzetben és önmagában. Kitalált dolgokat árul, és saját maga által kitalált szabályokkal. A szabályok dogmák. Ha el akarsz térni tőle, akkor egy új matematikai irányt / vallási szektát kell alapítanod. Persze a matematikák, nyelvi rendszerek hasonlat, már sokkal pontosabb.
Azt ami a matematikában helyes, jellemzően nem a matematika találta fel. Pláne eleinte. Csak lemodellezték a valóságot (életet) és írtak rá kifejezés és kommunikációs kódokat. - Amelyek azért eléggé pontatlanok, hiszen egyik alma sem azonos egy másik almával.- Nem véletlen az sem, hogy a számítástechnikában sokfajta működtető módszer ( alap program, operációs rendszer kódolás) van, és azt számítógépes nyelvi rendszereknek nevezik.
Legyen itt kezdő ráébresztő tanpéldának egy mondat: "Ez egy álhír; Gödel nemteljességi tételei érvényesek. " - feladat: Igaz, vagy hamis a mondat / állítás? Továbbá ez egy bizonyíthatatlan igaz állítás, vagy bizonyított is?
Egy másik ráébresztő példa is indulásként bemelegítésileg: A matematikában szinte bármit be lehet bizonyítani teljesen helyesen és szabályosan. Csak az axiómák és az axiomatikus szabályok felvételén múlik. Így a 2,4+2,4=4,8 egész számra való kerekítési, megfelelő megjelenítési és műveleti sorrend szabály utasítással éppen ilyen. Ebben az esetben 2+2=5 és teljesen logikusan és szabályosan. Továbbá 1+1=10 a kettes számrendszerben és 6x9=42 a tizenhármas számrendszerben. (kettes számrendszerben: 1+1=10) // ( tízes számrendszerben: 1+1=2) // (összevetve: 2=10)???!!! A matematika éppen ezért nem igazán tiszta tudomány, - hiszen kitalált dolgokkal foglalkozik, akárcsak isteneiket tekintve a vallások - csak segédtudomány. Kell hozzá más, nála sokkal tisztább tudományág valóságban is tapasztalható alátámasztása a vizsgált kérdéskörökben, hogy valóban igaz, tényszerű és hasznos lehessen. Persze 2+2, akár három is lehet. A következőképpen 1,6+1,6=3,2 egész számra kerekítése, megfelelő megjelenítési és műveletsor utasítási szabállyal. Ebben az esetben 2+2=3 és teljesen logikusan és szabályosan.
Ezen feltárásom a matematikai formalizálás hibalehetőségeit és korlátjait érinti: Kurt Gödel (1906-1978) matematikus első nemteljességi tétele érvényes-e, vagy csak főként egy hamis dilemmára alapuló érvelési hiba? A matematikai levezetésekben, tétel alkotásokban szabad érvelési hibákat elkövetni? Tényleg csak két választási lehetőség van? Vagy van még több is? Nem kellene inkább ezt átsorolni a paradoxon példákhoz? Mint David Hilbert (1862-1943) egyik leghíresebb matematikus Grand hotel felvetése is oda van sorolva. Egyáltalán matematika ez, vagy csak igen butuska és ráadásul hibás filozofálgatás? Gödel különféle tételei egymást is cáfolják?
A szórakoztató tudományfilozófia irodalmi stílusban megírt témára keresek könyvkiadót, elsősorban elektronikusat és előzetes elképzeléseim szerint legalább három (magyar, angol és német) nyelven jelenne meg egy nyomtatott könyvben vagy e-könyvben. Könyv fő címe és a borító terve: IGe : Gödel Bukta /Dunut /Krapfel ... ábra három fánk a magyar összecsavarodó bukta, a többi sima fánk, cukormázas szöveg rajtuk körkörösen: .... IGAZ MERT HAMIS MERT ... persze ez is három nyelven. Hasonlóan mint a judokeresztény biblia körkörös érvelését ábrázoló képek. Ezen link mögött az egyik. Kezdhetjük persze csak egy nyelven is. Aztán majd a többi. Meg az itteni szöveg alapvető mondandójának megtartásával, akár jelentős átszerkesztést is elfogadok.
Igen sok könyv jelent meg már korábban a témában a világon és hazánkban is. Ezek közül talán ez a legsikeresebb:

Természetesen újságok, magazinok, tévécsatornák, bloggerek, vloggerek, youtuberek és podcasterek is ha érdekli őket a téma, feldolgozhatják nem csak egészben, hanem részeiben is ide való hivatkozással és esetleges kérdésekre is szívesen válaszok. Nem kivételek ez alól a tudományágak képviselői sem, csak a könnyed feldolgozás miatt nekik erősen szokatlan dolog lehet, hogy valami némileg humoros részleteiben, de attól még a lényegi mondandó megállja a helyét. Meg sokan zokon veszik, hogy egy körülbelül 90 éves tudományos tétel, ami valójában csak egy dogma volt, az most megdőlt, megbukott, vagy inkább helyesen lebukott. Ráadásul ilyen egyszerűen, ami negyedórás olvasást igényel csak, de a lényege a barkóba (barkochba) tanpéldámmal meg csak 30-40 másodpercet. Amit a teszteléseim szerint 14-15 éves gyerekek is megértenek. A lényegre érdemes koncentrálni, hogy ezen Gödel tétel a tudományosság és a logika alapszabályai szerint érvénytelen, mert egyébként az átlagemberi gondolkodás szemléltetése miatt direkt hagytam benne apróbb hibákat.

Persze egy ideje tudtommal illik megadni már a matematikában is, hogy milyen érvényességi rendszerben történik a bizonyítás, vagy a cáfolás. Mert ami az egyikben jó lehet, az a másikban meg nem. Ahogy Isten, logika is sokféle van. Ezen felül még fura módon nem csak a filozófia, de a matematika is bevezette a metalogika fogalmat. Brööüüüűűű.???!!! Nóóóóómáááális??? !!! - Nos jómagam nem vesződnék ezzel, sem az elsőrendű, sem a magasabb rendű, sem a köztes, sem a deviáns logikával, mert a tudományosság, a logika és a helyes gondolkozás legáltalánosabb szabályait veszem alapul. Tehát valódi tudományosságát, vagy áltudományosságát vizsgálom. Ja és elnézést kérek azoktól akiknek fontos lenne kerülni, túl fontos is, de a közérthetőség miatt különféle ironikus és szarkasztikus szlengeket is használok. Másrészt a metalogikának kb. ennyi az értelme / értelmetlensége: A mesék is logikusak, a mese-logika szerint.
Gödel első nemteljességi tétele, egy matematikáról, fizikáról és csillagászatról szóló zárkörű csoportos facebook netes vita "agyvihar" jellegű része közben, egyértelműen megbukott 2021 novemberében. Bárki észrevehette volna előttem is, hogy az adott tétel csak egy trükkös átverés, becsapás, ami főként a hamis dilemmát használja. A hamis dilemma egy olyan érvelési hiba, amely úgy állítja be a vitát, mintha csak két alternatíva létezne, mikor valójában több, nem mérlegelt választási lehetőség is van. Ha az érvelésben ilyen hiba van, akkor a logikában és a tudományban érvénytelennek mondják és annak is számít. Kurt Gödel trükkje, vagy hibája: Tehát eleve három alternatívából, vagy döntési helyzetből indít, mert tudja azért, hogy a matematikai logikában vannak köztes állapotok is, így 1. paradoxon ( vagy eldönthetetlen, megoldhatatlan, önellentmondásos, egyik sem, is ) , 2. igaz (vagy nem cáfolható) és 3. hamis (vagy nem igazolható). Aztán kiveszi a paradoxont, tehát a hármat leszűkíti csak két alternatívára és megállapítja, hogy még is maradtak bent paradoxonok. Persze nyugodtan lehetne négy, öt, vagy hatféle dolog is - mert például paradoxonokból is két alap fő fajta van - ... ami mind igazolható, bizonyítható, hogy az és pont az. A matekban nem akadály bármit elnevezni valaminek. Lásd az "i"-t erre jó példának. A feladat lenne, aki szeret a mateknak azon részében molyolni, amit - az élő nyelv kiiktatását- még csak úgy kb 120-140 éve találtak ki (és a matek sötét oldalát jeleníti meg) - ezt itt lent, tehát a Hamis Dilemma logikai hiba formalizálását és Gödel első nemteljességi tételét összevetheti. Matematikai formalizálás tehát az, amikor a nyelvi mondatokat behelyettesíti valaki képletekbe. Egyébként megírhatnám matematikai formalizált nyelven is a feltárást Gödel első nemteljességi tétel érvénytelenségéről, hogy az alapvető tudományos elvekbe ütközik. Felesleges, de ha még is megtenném, akkor ez lenne a kiindulási alapja:
Valójában tehát nem is kellett cáfolni Gödel nemteljességi tételeit, de azért megtettem 5-6 féleképpen is, mert azok a tudományosság mércéi szerint nem is kerültek soha sem valóságos bizonyított állapotba. Ön és mások becsapásának az esetével állunk csak szemben. Lényeget tekintve nem más mint posztmodern filozófia *** , amiről az egyik régi általam nagyra becsült fizikus, Bencze Gyula a magyar és valódi szkeptikus mozgalom a Tényeket Tisztelők Társasága ötletgazdája, indikátora és valódi szülőatyja is írt. Arról tudvalévő, hogy csak úgy blöffölve azt állítják egyesek, hogy értik és milyen jó. Persze azért jónéhány ilyen kamu támogató időnként lebukik, hogy valóban értené. Például a Magyar Tudományos Akadémia Rényi Alfréd Matematikai Kutatóintézete legalább egy vezető beosztású alkalmazott kutatója, akivel magánban és nyilvános helyen is vitáztam már, és sajnos a hajdani már elhunyt St. Hawking is. Megjegyzem még: A Tényeket Tisztelők Társasága (1992-2006) utáni és abból kivált és átalakult, jellemzően harcos ateistákkal alapított Sz.eptikus Társaság egyébként ironikus megítélésem szerint lényegét tekintve nem más, mint egy szakértői álca nevezetű érvelési hiba.
Többek közt Ludwig Wittgenstein (1889-1951) filozófus, matematikafilozófus, nyelvfilozófus, logikus a munkáiban viszont a nemteljességi tételt helyesen látta: "logikai trükkökre jó". Valóban arra is lett használva. Wittgenstein Gödel "bizonyítékát" másokat, többen közt egyes matematikusokat is megtévesztő paradoxonként értelmezte.
Sokan mások is írnak hasonlóakat: "Gödel nem-teljességi tételének bizonyítása egy önmagára hivatkozó matematikai kifejezés felírásán alapul, hasonlóan az Epimenidész paradoxonhoz.” - Tautológia? (Duglas Richard Hofstadter (1945 -), kognitív tudomány.
Sőt a netes fórumos társalgásokban is rátapintanak a lényegre: "Szemléletes példája annak, hogy minden krétai matematikus hazudik. De mit kezdjünk vele, ha ezt egy krétai matematikus mondja? Ha a tétel teljes, akkor önmagáról bizonyítja, hogy nem teljes."

Másrészt Gödel ezen tétele körkörös hivatkozás is egyben és nem csak hamis dilemma. Miért? Mert önmaga bizonyítja önmagáról, hogy még sem sikerült elérni az eredendő célt, hogy konzisztens, eldönthetetlen állítás mentes, azaz önellentmondásmentes rendszer legyen a levezetés. "Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan állítás, mely se nem bizonyítható, se nem cáfolható." Kizárja az eldönthetetlenséget / ellentmondásmentességet és végül bizonyítja, hogy még sem felel meg annak. Tehát nem is lett kizárva. Gödel ezen tétele ezért nem más, mint csak egy plusz jó példa a paradoxonokra. Hasonló, mint David Hilbert Grand Hotel paradoxona, ami persze csak egy gondolatkísérlet és a valóságban nem is működik. Nem is lenne tehát semmi gond Kurt Gödel ezen paradoxonával sem, ha annak is neveznék. Továbbá Hilbert és sok más híres matematikus is több írásában hangsúlyozza, hogy egy feladat megoldhatatlanságának bizonyítása legalább olyan jelentőségű lehet, mint a pozitív megoldás. Középiskolában is elfogadott matekfeladat megoldása és bizonyítása afféleképpen, hogy nem bizonyítható. Ami persze azt is jelenti, hogy nem is cáfolható egyben. Hilbert egy okos matematikus volt, Gödel erősen korlátolt. Ez az egész, ideológia okok (teizmus < - > ateizmus) miatt félre van magyarázva. Hilbert sokkal inkább tisztában volt a matematika korlátjaival, viszont amire képes, azt ki akarta maxolni belőle. Helyesen látta Gödel tételeit is, hogy semmi jelentőségük sincs.
Ezt többek közt Bertrand Russel (1872-1970) filozófus és matematikus is felismerte a zárt logikai rendszerek körkörösségi érvelési hiba önellentmondását, az önmagát borotváló meg nem is, borbélya paradoxon tanpéldájával. ( Ami persze, egy női borbély esetén kissé más értelmezést kapna.)
Az is fura, hogy a matematikusok ezen 'tétel' kapcsán csak az önellentmondásra és annak kiküszöbölésére koncentrálnak, holott van ezen kívül még számos más logikai hiba is, ami miatt egy bizonyítás érvénytelen, vagy elfogadhatatlan, vagy lehetetlen. Illetve nem teljes. Ez a folyamat meg lefedi a nem igazi skót érvelési és logikai hibát. Ami egyben mazsolázgatás nevezetű érvelési hiba is. Vagyis önkényes kiválasztás a tudományos elvek közül. Holott ilyet nem lehet tenni. Mindet be kell tartani.
"A metafizikusokon és pozitivistákon kívül azonban van a fizikai világkép kialakítóinak egy harmadik csoportja is. Jellemző rájuk, hogy érdeklődésük nem irányul sem a reális, sem az érzéki világgal való kapcsolatra, hanem inkább a fizikai világkép belső zártsága és logikus felépítése felé. Ezek az axiomatikusok." Max Planck: Az új fizika világképe. A matematika jelentős része axiomatkus és a fizika is megfertőződött vele. A legjobb példa erre a monoBigBang hiedelem és tudományos tévhit. Szerencsére nem minden része.
Gödel 2. nemteljességi tétel: " ... az egyik ilyen eldönthetetlen és bizonyíthatatlan állítás, pont az hogy a rendszer ellentmondásmentes" ..." Értelmezés szerint - és ez minden bizonnyal egy helyes értelmezés- már cáfolja is vele a saját korábbi hasonló nevű, csak éppen egyes sorszámú tételét. Lehet nem is egyet, hanem kettőt is. Tehát a teljességit is.
Kurt Gödel matematikus volt képzettsége szerint, de igazából filozófia jegyzeteket és könyveket írt. "Gödel nagy filozófus akart lenni Platón, Leibniz és Kant hagyományát követve." Négy tétele / érve az ami híresebb. 1. Matematikai teljességi tétele 2 Matematika első nemteljességi tétele 3 Matematikai második nemteljességi tétele 4. Matematikai formalizált nyelven megírt ontológiai istenérve. Minden jel szerint és bizonyítottan, ezek egymást is cáfolják.
Vicces és roppant önellentmondásos ez a "nem bizonyítható" dolog is. Mert ha nem bizonyítható, akkor hogyan is lett maga ez a tétel bizonyítva, és az is hogy éppen nem-e ebbe a "nem bizonyítható" részbe esik? Nekem az erősen azonos azzal, mint amikor valaki kijelenti, hogy "Ízé" azaz a nagy "I" kívül áll a felfoghatóságon. - Ja és azt, hogyan lehet felfogni, hogy a nagy "I" felfoghatatlan? Vagy a felfoghatatlanság még is a legfelfoghatóbb?

(-1) x (-1) = 1 azonos elven (-Isten) x (-Isten) = Isten ???? Hahahahahaha :-)
Közben kiderült, hogy a mínusz egy gyökvonása sem értelmetlen már, legalább is a matematikusoknak, holott sokáig paradoxonnak, vagy önellentmondásnak számított náluk is. Mára már arra is van axióma, vagy nem is tudom mi, de reális definíció az aligha lehet. Tehát ma már az a matematikai kis "i". Segédmarhaság, talán ez a legjobb kifejezés rá. Jómagam ezt mint alkalmazott mérnöki tudományban is képzett, inkább elrettentésül tanultuk, mint "nem hasznos" és nem is használható tudást. Nekünk inkább valós világunkon kívüli oximoron (önellentmondó képtelenség) volt. Később tudtam meg, vettem észre, hogy ehhez Leibnizen kívül, Eulernek is köze van.

Pszichovirulógiailag persze nincs ebben semmi fura, hiszen a matematikához erősen hasonlító egyik vallásban XY " kitalált zombifigura" egy darabig nem volt Ízé, azaz "I", azaz "Isten", aztán szavaztak róla és ~316 igen, kettő nem mellett meg lett szavazva és attól kezdve már az. Az nem nagyon zavarta szavazókat, hogy az egyistenhitükben eggyel több "Isten" lett a kelleténél és illendőnél. A matematikusok meg négyzetre és köbre is emelik a "végtelent" is. Bár némelyik azért belereccsent ebbe mentálisan régebben.

Megjegyzek egy olyan összefüggő érdekességet, miről szintén híres Kurt Gödel és hát azzal nem kicsit vitte bele a matematikát népiesen a "susnyásba" vagy az áltudományba. Persze a dolog sok néző és álláspontból vizsgálható, de a tény, hogy írt és végzett egy formalizált logikai, matematikai nyelven "Ízé" azaz Isten elemzést. - Milyen érdekes egybeesés. Lehetne ez a nagy "I" a kis "i" mellett. - Avagy istenérvet. Saját és mások megfogalmazásában bizonyítást. Az is igaz, hogy ezt hivatalosan nem publikálta*, de ismerősei átal viszont kiszivárogtatta. Tehát ma már tudunk róla és fura módon sokan ezt érvényesnek és helyesnek is tartják. Persze főként csak a teológiában, a matematikában tudtommal nem és ignorálják is, mintha nem is lenne ilyen. Gödel matematikai elemzése, némileg Leibniz általi átdolgozott verziójú, de lényegében akkor is Anzelm (Aosta, Olaszország, 1033 – Canterbury, 1109 ) szöveges 'érvelésének' az átvitele matematikai axiomatikus formalizált nyelvre. Ami tény, hogy Anzelm korában nem is létezett, hiszen azt csak úgy cirka 800 évvel később találták ki. Persze az is tele van hibákkal és nem érvényes. Már csak azért sem - mert Anzelm istenérve is - sokféleképpen és sokkal által megbukott. Lehet elemeznem kellene részletesen itt és szájbarágósan azt a kettős mércét is, amivel a teljesen azonos felépítésű két Gödel formális matematikai levezetés közül ( első nemteljességi tétele vs ontológiai istenérv bizonyítása) az egyiket egyesek elfogadják helyesnek, a másikat meg már nem. Pedig Gödel végső konklúziója azonos jellegű mindkettőnél. Amit szóban közölt, azt a formalizált matematikai nyelvvel is bizonyítottnak vélte. Tegyük ide a Gödel ontológia istenérv hókuszpókolását is egy képen szemléltetve:
Egy adott vallás előírásait, vagy Gödel tételét jónak és helyesnek vélni, csak egy hibás emberi pszichés állapot. Kutatásim és teszteléseim alapján, egyik ellen sem működik / hatásos a racionális érvelés. A legtöbb matematikus csak hajtogatja a matematika-vallás egyik dogmáját, hogy a Peanó eljárással beszűkíteni a lehetőségeket, ( két választási lehetőségre) az szabályos. Szemléletes példával ez hasonló, hogy csak egy "Istened " lehet és nem több.
Gödel tételei hasonlóan és memetikusan terjedtek el, mint a vallások és az "Isten" kultusz. Támogató mémje, az "Isten" mémnek. Lásd: Glenn Grant: Memetikus lexikonját. "co-mém: Egy mém, mely szimbiózisban fejlődött együtt más mémekkel, hogy kialakítsanak egy egymást kölcsönösen támogató mémkomplexet."
Természetesen ha jobban belegondolunk, akkor a gyakorlatilag Kurt Gödel egyik tétele sem matematika, hanem csak filozofálgatás. Filozófiai állításokat helyettesített be formalizálásba, magyarán csak kódolni próbált ... és hát nem túl jól.

Eleve a zárt axiomatikus rendszerek a komolyabb és valódi tudományfilozófiában és a logikában is vicc kategóriák. Mert ugyebár vannak különféle érvek és több lépcsős levezetések X létezésére , vagy X igaz bizonyítására ... de elég egy axióma is. X létezik, vagy X igaz. A REÁLIS DEFINÍCIÓ és definiálás menete, amire a valódi tudomány épül az nem AXIÓMA és nem axiomatikus !!!! Mert a reális definiálás már egyben egy bizonyítási eljárás is. - Itt ugye az volt a gond, Gödel ontológiai istenérvénél, hogy egy alap axiómát már az emberek nem hittek el, hogy igaz lenne. Mert bizony az alap axiómák sokszor csak hitre épülnek és semmi másra. Másrészt meg pont itt kezdődnek a gondok, tehát az axiómákkal, amelyek ugye nem REÁLIS DEFINICIÓK, hanem csak "ALAPIGAZSÁGOK", amelyeket megkérdőjelezni sem szabad, tehát nem is lehet dönteni róla, hogy igazak-e, vagy sem. A matematikai axióma "alapfeltevés", "alapigazság" azaz DOGMA. Azaz nem bizonyított. Azaz nem tudományos. Tehát már maguk az axiómák is "se nem bizonyíthatóak, se nem cáfolhatóak". - Spanyol viasz felfedezése a folyamat ugye... Kék az ég és zöld a fű ... szerű. Hiszen az axióma fő tulajdonságai már Eukleidész matematikai tankönyvében, és Arisztotelész írásaiban is olvashatóak.
A valódi tudományterületek éppen ezért nem is axiomatikusak, hanem reális definíció, vagy csak elnevezés alapúak. A reális definíciók és az elnevezések viszont vitathatóak.
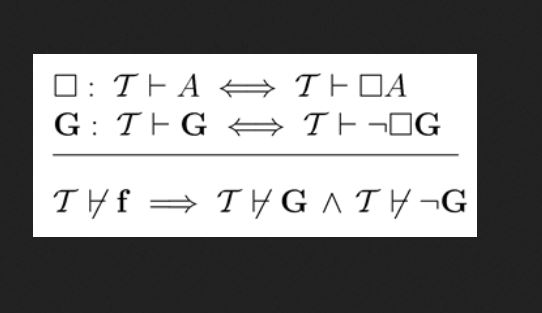
Tegyük ide egy képben a gödeli nemteljesség ámítását is matematikai formalizált nyelven, ami meglepően rövidke és hiányos is. Akkor is ha az 1930-as publikációjában 27 oldalt írt még mellé töltelékszövegként. Eleve bizonyítani kellene azt is, hogy az ő saját tétele nem tartozik-e abba, amit felvet. Mert ugye akkor a jó körkörös érvelési hiba, ez előzővel együtt már kettőzötten is, ami latinul: Petitio principii. Már ezen ok is gyanút adhatott volna a sokkal korábbi felülvizsgálatra. Lényeges, hogy ezt már a görög filozófusok bizonyították 2,500 évvel Gödel előtt. Az a tény, hogy ezt formalizálta, nem ad hozzá semmi extrát. Kb olyasmi mint valamit átfordítani egy másik nyelvre is.
Másként is megfogalmazva ezt a gondolatot: Gödel nemteljességi tételei a matematika saját 'tanmesevilágában' járnak csak és semmilyen jelentős hatással nincsenek a tudományra. Egy zárt rendszer belső dogmája csak. Miért? Mert FORMÁLIS axiomatikus (kitalált) dolgokat elemez és arról ír szabályokat. A tudományban meg REÁLIS definiálások (bizonyítottak) szükségesek. Ütközik a tudomány más, és általános szabályaiba. Azon kívül is a 'megállapításai' banálisak és semmi újdonságot nem tartalmaznak, amit addig már ne tudtunk volna. Oximoronok és paradoxonok már eléggé régiek. Már az ókori görög tudósok is értekeztek mindkét dologról olyan cirka 2500 évvel ezelőtt is. Sőt a halmazelmélet alapján, abban a gödeli korban, tehát úgy 1930 környékén, már a két halmaz közös része sem ismeretlen dolog. Tehát az IS.
Értelmező hasonlat: Ha egy elv (levezetés, bizonyítási kísérlet stb) csak a teológiában, vagy a metafizikai filozófiában (ebbe beleértve az ateizmust is), és annak belső szabályaik szerint helyesek és máshol és általánosan nem, akkor az bizony áltudományos elv. Egy olyan megállapítás és levezetés a teológiában, hogy csak a saját "Isten"-ük, amely neve Jahve Isten az valóságos és logikus, de a többi Aton, Hórusz, Mithrász, Dionüszosz, Attis, Krisna, Visnu, Baál, Thor, Wotan, Borvo, Marduk, Allah, Ré, Zeusz, Siva, Dyḗus, Ahura Mazdá, Nagy Manitu ... nem az, dettó áltudomány. Sem a logika sem annak egy eleme nem kisajátítható és csak "egy van belőle és az övék az igazi"**- vá sem tehető. Sőt az Isteneket (lásd Isten összeszámlálás), tehát a sok-sok Isten tényét sem lehet Hamis Dilemma érvelési hibával leszűkíteni; hogy "Isten létezik" és "Isten nem létezik" lehetőségek közül lehet csak választani.
Gödel nem teljességi tétele, meg még egy zárt rendszeren belül is, külön is bezárt dolog. "Fontos megjegyeznem, hogy Gödel tételei csak a matematikai rendszerek egy részében érvényesek, nem alkalmazhatóak a számokat vagy a formális nyelvezetet nélkülöző euklideszi geometriában, humán és társadalomtudományokban vagy bármely hasonló rendszerben." Bővebben és teljes terjedelemben meg itt olvasható.
Tehát Gödel ezen tételei megbuktak, mert az általános helyes érveléstan alól a matematika sem lehet kivétel. Gödel meg a hamis dilemma érvelési hibát igen ügyesen elrejtette. Észre lett véve, így bukott. Továbbá mint írtam, saját magát is buktatja ... és ha még tovább gondoljuk, akkor azt láthatjuk, hogy még a matematikai formális axiomatikus rendszeren belül, a hamis dilemma hasonló módon végzett formalizálása is kiüti.
Ez a legtömörebb lényeg: Gödel első nemteljességi tétele sérti a helyes érvelés szabályait és főként hamis dilemma alapú érvelési hibát tartalmaz, de fellelhető benne a körkörös, mazsolázgatás, nem igazi skót és a szakértői álca nevezetű érvelési hiba is. Továbbá az újdonság hiánya is szemére vethető, hiszen az oximoronok és a paradoxonok már legalább 2500 éve feltártak és ismertek. Számos, akár 5-6 ok miatt is elvetendő a tudományban. Így valóságban ez csak egy a többitől némileg eltérő paradoxon tanpélda. Így az emberi gondolkozás és logika evolúciójának egy fontos része, de már kinőhető és túlhaladható. Megmaradhat, mint tudománytörténet.
Ezen kívül még számtalan módon le lehet vezetni, hogy miért nem jó és helyes és igaz. Most már tényleg csak plusz egy variációt rakok be ide bővítésként, mert a kezdeti szöveg már kb négyszerese lett és az emberek röviden szeretnek tájékozódni és nem hosszasan. Ezt az index fóruma tudomány rovatában a Gödel és a teljesség topikjában lévő tesztelés és vita egyik felvetésem ott: Gödel első nemteljességi tétele nem tudományos tétel, hanem áltudományos. Ugyanazokat a trükköket használja az ELHITETÉSRE mint a judeokeresztény teológusok és apologéták. Bármennyi formális axiómát és döntési válaszokat is lehetősége lenne felvenni. A teológusok is bármennyi "Ízé" formális axiomatikus variációt elemezhetnének. .... de nem, a teológusok ÖNKÉNYESEN kizárnak más "Ízé" -ket és csak a sajátjukat elemzik. Gödel is kizár más AXIÓMÁKAT és válaszokat és csak azt elemzi, amivel szédíteni tudott. Sőt a teológusoknak módjában lenne nem formális axiómákat elemezni, hanem REÁLIS DEFINÍCIÓT is. ... de azt is kizárják. Semmi más tehát mint a logikus és következetes gondolkozás kizárása, azaz áltudomány Gödel ezen tétele. Még pontosabban megadva: áltudomány, álfilozófia, álmatematika.

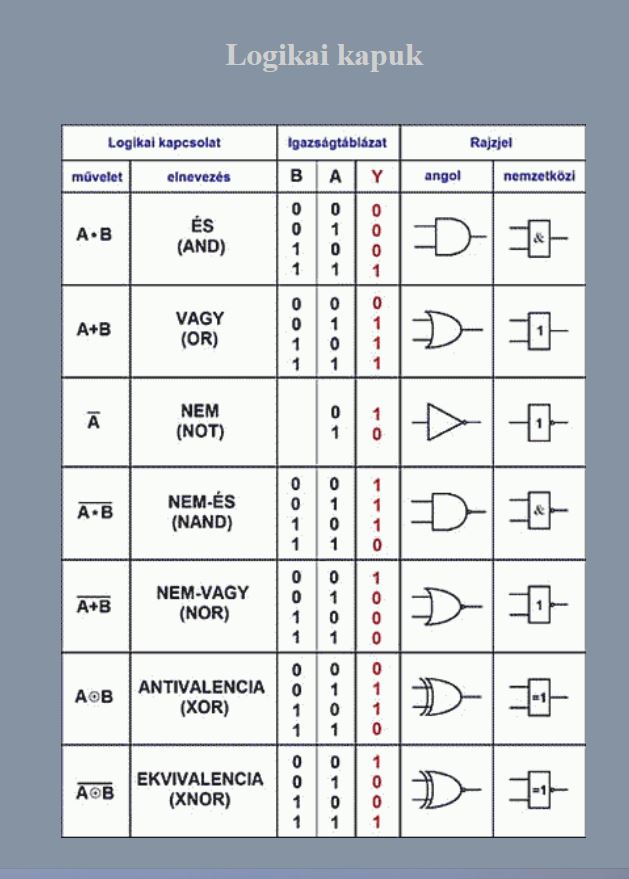
Összesen hétféle logikai kapu létezik, melyek igazságtáblája különböző. Tehát kettő nem elégséges. Ezek az AND, OR, NOT, NAND, NOR, XOR, XNOR. A hét kapu mindegyike csak kétféle kimenetet produkálhat. " Logikai kapukkal végzett műveletekkel, a Boole-algebra alkalmazásával minden matematikai feladat megoldható." - wikipédia
Na jó még sem álltam meg és berakok még egy banális cáfolási módot:
Gödel első nemteljességi tétele is pszihovirus-szerűen (vallás/hit, konteó, álhír, fake news, hiedelem, áltudomány, posztmodern filozófia, téveszme, pletyka ...) terjedt csak el, mert az is csak érvelési hiba trükk, átverés, akárcsak más átverések, amelyek még is népszerűek. Lásd kijózanító példának a barkochba találgatós játékot és kétféle szabályrendszerét. Az alap barkóba axióma és belső szabály-rendszerében csak IGEN és NEM válasz lehet. A kibővített barkóbában meg IGEN, NEM, IS, NEM JELLEMZŐ és NEM TUDOM. Mindkettő axióma rendszer és belső szabályok összessége. Sőt mindkettő formális axióma rendszer. Tehát egy olyan rendszerben, amiben a szabályok és az axióma rendszerek is csak saját magán múlnak, az bizony körkörös logika. Elvi hiba és elvetendő. Vagy mindkettő barkochba. Mindkettő matematika, és akkor Gödel első nemteljességi tételére is felvehető egy kibővített axiómarendszer, amiben már működik a játék és teljes. A matematika tehát lehet TELJES !!! Aki ezzel a hasonlattal sem érti meg, miért hibás, az már tényleg a beteges mentális ragaszkodás egy marhasághoz jelenség. Tévhit kategória. Igen erős freudi elszólás az, akik ezt "in/nem-komplett"-ségi tételnek nevezik, :-) .... de végül is igaz ... valóban az. ( Magyar nyelvben a nem-koplett = őrültet jelent.)
"A Gödel tételben szereplő 'nem eldönthető állítás' egyszerűen azért nem dönthető el, mert eleve úgy lett megfogalmazva, hogy önmagának ellentmondjon. Abban pedig semmi csodálnivaló nincs, hogy egy önmagának ellentmondó, azaz logikai hibát tartalmazó állítás nem eldönthető. A Gödel tétel az ilyen 'patologiás állításokról' bizonyítja, hogy eldönthetetlenek - de ezt formalizálás nélkül is tudjuk." forrás (Geier János ELTE Pszichológiai Intézet, mellesleg alapból matematikus. Ja és szerinte Gödel ezen tétele csak a Richard paradoxon formalizálása.) Bővebb verzió itt: Gondolat 2004
Zhang Hong a matematika filozófiájának kutatója is, paradoxonnak értékeli csak, az egyik közzétett írásában.
Tehát az igazán nagy matematikusok, mindig is tudták, hogy a matematika, csak egy sajátságos valláshalmaz.
Friedrich Ludwig Gottlob Frege (1848 – 1925) német matematikus, logikatudós, filozófus "1923 táján arra a következtetésre jutott, hogy az élete java részét meghatározó elgondolás (a logicizmus), mely szerint az aritmetikát teljes mértékben a logikára kell alapozni, téves volt." forrás
A Tényeket Tisztelők Társasága 1998-as konferenciáról nagyon sok értékes előadást és előadót is kiemelhetnék, de most csak Frid Ervin matematikus megfogó szavaival teszem ezt. "Rossz az iskola rendszerünk...A gyereknek el kell hinni amit a felnőttek tanítanak... Babonára tanítunk... Az emberek bután tartása hasznos dolog, sokan csinálnak ebből hasznot... Tekintélyelvű a világunk... A tévedés jogát fenn kell tartanunk." forrás és bővebben
Beck Mihályt is megemlíteném, szintén az adott társaságból. Tudomány - áltudomány című könyvéből idézek.: "Nem szabad hamis illúziókat táplálnunk a tudományról: a tudományos igazsághoz vezető út jószándékú tévedésekkel van kikövezve."
Eddig nem is írtam, de remélem azt már tényleg ki tudja mindenki logikázni, hogy ha Gödel első nemteljességi tétele megbukott a tudományosság mércéi szerint, akkor velejárója, hogy a második ilyen tételének is ez a sorsa. Sőt attól tartok, hogy az úgynevezett teljességi tétele is hibás logikára épül. Bár azt még nem elemeztem. Mert eleve a matematikai formalizálás, mint helyes bizonyítási és érvelési módszertan lehetőségei erősen korlátozottak és rengeteg benne a hibalehetőség. Hatalmas hibalehetőség már az, hogy a sokkal több lehetséges és valós változónál csak egyes kiválasztott változókkal kalkulál és számol. (mazsolázgatás érvelési hiba).
A kitalálós játékban (barkochba) sem elég az "igen" és "nem " válasz (2), hogy működjön. Az a tapasztalat, hogy minimum öt (5) kell. A logikai kapuknál, több százéves tapasztalat (Boole-algebra), hogy minimum hét (7) döntési helyzet, az amivel a matematika (számítástechnika, irányítástechnika) lefedhető. Tehát Gödel nem is fedte le, a matematikai döntéseket, teljességében. Csalt / trükközött !!! Hét helyett, kettőre szűkített.
Tudománytörténeti tény. Fél, de inkább az egészhez nagyon közeli, matematikai szakterületi szakma, azon rőkönyödött meg és röhögött, amikor Gödel már a matematikai formalizálást is formalizálta. Csak számokat akart használni. Ez már nem is ment át, ez már akkor megbukott. A matematikában. Ez viszont Neumannak segített a számítástechnikában. Mert paradox módon a Gödelnek a Gödel-számozás / kódolás volt az egyetlen használható elmélete. Aminek volt gyakorlati haszna is. Persze csak eleinte a számítástechnikában. Amikor még minden karakterrel és bittel spórolni kellett. Nos ami hasznos volt, pont az bukott meg a matematikán belül. Ami meg haszontalan és téves, azt meg oltárra emelték.
Tesztelés: Ja örömmel veszem az érdemi kritikákat ezen Gödel nemteljességei tételeinek, az általános tudományban és logikában való érvénytelenségének felismerését és kimutatását illetően, ha esetleg a lényegi kérdést illetően pontatlan lettem volna vagy tévednék valamiben. Persze, csak az ha betartja a vitakultúra, a helyes érvelés és tudományos módszertan szabályrendszerét. Apróbb hibák nem érdekesek, mert mint jeleztem, ilyet direkt hagytam benne néhányat.
Bővítésekkel és apróbb folyamatos javítgatásokkal és pontosításokkal ellátott P-Dox Semmiben Sem Hívők vallás időszámítása (+40 ezer év a mostani még hivatalos Eu-hoz ) szerinti 42 023. március 14.-i változat. Később is tettem benne még néhány apróbb változtatást, betoldást, de a dátumot memetikai okokból már nem módosítom.
Meg kell jegyeznem, hogy Gödel ezen tételét már a kortársai is cáfolták. Köztük Russel és Hilbert is bizonyította, hogy ez csak egy banális és régen tudott dolog. Csak valamiért nem figyeltek rá eléggé, kultusz lett. + 'A matematika igaz, mert a matematika azt írja.' Azaz Gödel újra felfedezte a spanyol viaszt, vagy a Petitio principiit.
Ezen bizonyítást számos helyen tettem ki kritikai próbákra és álltam és állom is azokat. Ez a legutóbbi egy 420 ezer fős nemzetközi és angolnyelvű csoportban történt.
Lényeges elem még. Mert ez a kutatási folyamat vezetett ide is. : A logika és az emberi agy ( elme ) hibáit is kutatom. Gödel tételei csak mémek. Vagy sokkal tudományosabb kifejezéssel; pszichológiai vírusok. Tehát megbetegítéssel és fertőzéssel terjedtek el. Nem a tudományos módszertan alapján. Gödel semmit sem bizonyított. Egy zagyvaság, tautológia, paradoxon, oximoron, heideggeri posztmodern filozófia az amit össze firkált. Amiben alap érvelési hibák vannak, az nem tudomány, nem is filozófia. Gödel tételei max vallásnak jók. Ott nem kell betartani a helyes érvelés szabályait.
------------------------------------------------------------------------------------------------
Függelékek, kapcsolódó gondolatok, értelmezések:
Akik szerint a Gödel-tétel alapvetően logikailag hibás;
1. David Hilbert (1862 –1943) matematikus
2. Bertrand Russel (1872-1970) filozófus és matematikus
3. Ludwig Wittgenstein (1889-1951) filozófus, matematikafilozófus, nyelvfilozófus, logikus
4. Douglas Richard Hofstadter (1945 -) kognitív tudomány
5. Geier János ( ... ) matematikus, pszichológus
6. Zhang Hong ( ... ) a matematika filozófiájának kutatója, egy írása
7. Iván Gábor elemér - IGe ( 1966 - ) robotikus, logikakutató
8 . John D. Barrow (1952 -2020) angol kozmológus, elméleti fizikus és matematikus ?

* Raffai Péter asztrofizikus ezen videószereplése szerint (51:34 től) még is publikálta 1941-ben valahol >de nem nevezik meg pontosan hogy hol.
** Azaz a nem igazi skót érvelési hiba. "Azzal, hogy kizártál bizonyos alanyokat abból a halmazból, amelyre kijelentéseid igaznak tartod, valójában nem megvédted az eredeti állítást, hanem elismerted annak téves mivoltát, és helyette egy új, szűkebb érvényességű, tehát eltérő tartalmú állítást fogalmaztál meg." - forrás
*** magyar népies kifejezéssel parasztvakítás
**** Már csak azért is mert Gödelnek van teljességi törvénye is a matematikára. "Gödel teljességi tétele a matematikai logika fontos tétele, azt mondja ki, hogy ha egy elsőrendű elméletben egy tetszőleges mondat minden modellben igaz, akkor bizonyítható is."
+ A matematika egésze Gödel előtt is részben zár és részben nyitott logikai rendszer volt és most is az.
Zárt ~ axiómák (formális definíciók), dogmák, saját törvények, nincs átjárás más tudományokba, tesztelhetőség elvetve, egyénileg, vagy szavazásos döntések, tekintély elvek ... áltudomány jelleg
Nyitott ~ reális definiálások, általános törvényszerűségek, más tudományokkal is összhang, széles körű tesztelés, bizonyítással és annak is a + próbáival való döntés, tekintélyelv elvetése ... valódi tudomány jelleg
Jelenleg is a tudományágaknak besoroltak szinte mindegyike ilyen vegyes felállásban van. Van olyan ami szinte teljesen Zárt és áltudomány jellegű és inkább csak max ISMERET, és olyan is amely szinte teljesen Nyitott és tudománynak mondható. Ja és igen a valódi tudományban ott a fejlődés is és a dolgok idővel átértékelődhetnek.

+ Ajánlott irodalom:
POSZTMODERN PANOPTIKUM , Magyar Tudomány, 1998. december Bencze Gyula
posztmodern módra Bencze Gyula KFKI Részecske és Magfizikai Kutató Intézet
+ tudomány; A tudomány egy a tekintélyelv elvető módszertan, aminek az alapja a logika, az ok okozati összefüggések, a helyes érveléstan és a bizonyíthatóság. Fő eleme a kritikai vizsgálat és a tesztelés. A tudomány módszertana, ha valami nem működik leírásának megfelelően, akkor pontosítja azt, vagy elveti.
+ Írtam erről egyébként még egy Dialógus jellegű utórezgést is, ahol Gödel esetleges rejtjelezett üzenetéről elmélkedek.
Volt három megelőző előrezgése is: 1. Gödel ontológiai istenérvének a cáfolata 2 .Gödel az elmebeteg tudós 3. Hawking és Kurt Gödel első nemteljességi tétele
10 Gödel tétele
20 igaz, mert hamis
30 hamis, mert igaz
40 GO TO 20
+ A Gödel első nemteljességi tételének a hozzá fűződő szöveges magyarázataiból "az igaz, de nem bizonyítható" rész amit a legjobban szeretnek a teológusok és egyes asztrofizikusok is kimagyarázásnak, akiket logikai hibákon kapnak. Ez itt a saját feltárásomban is okozhatna némi ellentmondást, ha az igaz lenne és nem csak valamiféle halandzsa. - Meg ugye, akkor Gödel tétele is pont ez lenne??? ... Akit ez esetleg zavar, annak javaslom azt a részt hagyja ki és csak a többi és más jellegű érveléseimet elemezze.
+ Egy axiómákra épülő ZÖLDSÉGBŐL, csak akkor lehet TUDOMÁNY, ha az átmegy a REALÍTÁS és RACIONALÍTÁS mércéjén is. Tehát + empirikus bizonyítások és alátámasztások is kerülnek mellé. Különben csak max tanmesék, amik lehetnek jók valamire vagy sem.
+ Mi ez a rejtélyes hasonlóság vajon a két körkörös logikai hibát tartalmazó mondókában? ;
1. "Minden ellentmondásmentes, a természetes számok elméletét tartalmazó, formális-axiomatikus elméletben megfogalmazható olyan állítás, mely se nem bizonyítható, se nem cáfolható."
2."Isten egyértelműen kívül fekszik a tudomány hatókörén. Nem lehet sem bizonyítani, sem cáfolni."
+ Belekeverhettem volna az elemzésembe a többértékű logika elméleteket is, de banálisak és a végeredményt illetően semmit sem változtatnának.
+ "Kurt Gödel érdeklődése 1943-tól kezdve fordult a filozófia felé. Eleinte a matematika filozófiai kérdései foglalkoztatták, a leghíresebb - publikált - tanulmányai e téren a Russell matematikai logikájával ill. a Cantor-féle kontinuum-hipotézissel foglalkozó írások." https://epa.oszk.hu/00100/00186/00001/98_csaba.htm
+ Tisztában voltam és vagyok vele hogy a matematikai formalizálás formalizálásának a matematikában nincs értelme, mert csak érthetetlenné bonyolít, szinte már rejtjelezés. A gépeknek ez nem gond és ott lehet hasznos. Jómagam is végeztem hasonló kódolásokat és felprogramozásokat is régebben.
+
Proof that Wittgenstein is correct about Gödel
When we sum up the results of Gödel's 1931 Incompleteness Theorem by formalizing Wittgenstein’s verbal specification such that this formalization meets Gödel's own sufficiency requirement: ”Every epistemological antinomy can likewise be used for a similar undecidability proof." then we can see that Gödel's famous logic sentence is only unprovable in PA because it is untrue in PA because it specifies the logical equivalence to self contradiction in PA.
Bizonyíték arra, hogy Wittgensteinnek igaza van Gödellel kapcsolatban
Amikor összefoglaljuk Gödel 1931-es hiányosság-tételének eredményeit Wittgenstein szóbeli specifikációjának formalizálásával, hogy ez a formalizáció megfelel Gödel saját elegendőségi követelményének: „Minden episztemológiai antinomia hasonlóan felhasználható hasonlóan a megdönthetetlenségi bizonyításhoz. "akkor láthatjuk, hogy Gödel híres logikai mondata csak PA-ban bizonyíthatatlan, mert a PA-ban nem igaz, mert a PA-ban meghatározza az önellentmondással való logikai egyenértékűséget.
(PDF) Proof that Wittgenstein is correct about Gödel (researchgate.net)
+ Friedrich Ludwig Gottlob Frege (1848 – 1925) német matematikus, logikatudós, filozófus 1923 táján arra a következtetésre jutott, hogy az élete java részét meghatározó elgondolás (a logicizmus), mely szerint az aritmetikát teljes mértékben a logikára kell alapozni, téves volt.
+ A műszaki alkalmazott mérnöki tudományban fontos eljárás: Egy mérés nem mérés. -> Egyfajta bizonyítás, nem bizonyítás.
Tehát Gödel tételeit, csak a matematikai Peanó-féle "logika" alapján értelmezni, nem elegendő. Kellenének más módon való alátámasztások is.
+ Összesen hétféle logikai kapu létezik, melyek igazságtáblája különböző. Ezek az AND, OR, NOT, NAND, NOR, XOR, XNOR. A hét kapu mindegyike csak kétféle kimenetet produkálhat. " Logikai kapukkal végzett műveletekkel, a Boole-algebra alkalmazásával minden matematikai feladat megoldható." - wikipédia



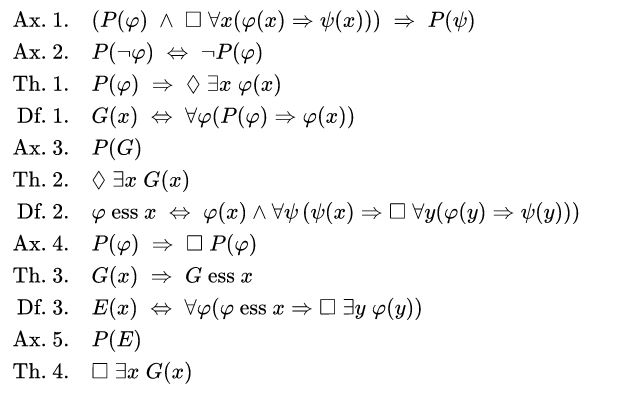

Az utolsó 100 komment: